For too long the EDM world has overlooked music theory, or only superficially skimmed the surface.
So I made this guide – a comprehensive, in-depth look at music theory and how it applies to electronic music production. I’ve made posts as concise as digestible as possible. In other words, this is Music Theory: The TL;DR version.
This series is going to be divided into parts:
- The fundamentals (aka, this post and its articles)
- Intermediate/advanced ideas and composition tricks
- The overlap of theory and production
I’m particularly psyched to get to the third point; It’s a relatively unexplored area.
So, without further ado, let’s go!
Understand music theory without spending years learning the hard way 🎶
Grab our free 87-page eBook, Music Theory: The TL;DR Version – nail the fundamentals of melodies, chords, and notes the simple way 👇
Table of contents
Why Music Theory Matters
Composing without music theory is like mixing a song without EQ. It’s possible, but I wouldn’t recommend it.
The main problem with ignoring theory is that, chances are, you’ve grown up surrounded by Western music. And your ears probably prefer Western music.
So the music you inherently prefer will follow the rules of Western music. And by “rules of Western music,” I mean music theory. To break the rules, you have to realize you unconsciously follow them.
It’s been said on this site before that you can’t polish a turd. My own personal iteration of this is “grimy gold is worth more than shiny shit.” The best mixing techniques and experience won’t fix a mediocre composition. Music theory, on the other hand, can.
A tip on “studying” the concepts I’ll discuss: use them. Write songs for the sole purpose of exploring diatonic chords, or do whatever you need to do to make things stick. Just use theory in any way you can and push into territory you’re uncomfortable with as often as you can.
TL;DR: STFU and learn music theory.
The Major Scale
There are two main scales formulas: major and minor.
Each is built on the concept of “steps,” which are either half or whole.
A half-step is the distance between a white key and the black key next to it on the piano. Or the distance of one fret on a guitar. The first two notes of the jaws theme are a half-step.
And two halves make a whole – add two half-steps together and you get a whole-step.
Here’s what a half- and whole-step sound like:
Side note: half-steps can be called semitones and whole-steps can be called whole tones.
And, of course, we can stack these steps on top of one another. I tell my guitar students to imagine a ladder.
Some steps in the later are 6 inches from the next, some are 12 inches. Stack a bunch of those steps together and you can climb to the next story of a building.
This is the idea behind a scale; steps are organized in such a way that they arrive one octave up. “An octave” refers to a note twelve semitones above another. It’s important to know that an octave is the repetition of the same note. C an octave up is C, right? It’s just a higher C.
With that in mind, here’s a major scale formula:
So what does that all mean? Here’s the way I notate it. A “^” means a half-step:
1 2 3^4 5 6 7^1
Notice, first of all, that I repeat “1” once the scale hits the octave. This is because it’s not a new note, remember? A “C” played an octave above another “C” is still a “C.”
Alright, so that formula shows you that there are two half-steps in the major scale. One is between 3 and 4, and one between 7 and 1.
On a piano, if you play a scale starting on C, you’ll notice the half steps line up with the places where no black keys are present. Two white keys without a black key in between them on a piano are a half-step apart. Or on an open guitar string, you would play the frets: 0-2-4-5-7-9-11-12.
TL;DR: Scales are built by stacking half-steps and whole-steps. The major scale is made of five whole-steps, and two half-steps: between 3 and 4, and between 7 and 1. It can be written like this, where “^” means half-step: 1 2 3^4 5 6 7^1.
The Minor Scale
There are two approaches to understanding the minor scale:
First, the minor scale is like the major scale. It’s made of five whole-steps and two half-steps. However, the steps are arranged differently. It can be written like this, where “^” means half-step:
1 2^3 4 5^6 7 1
The half steps in a minor scale fall between 2 and 3, and 5 and 6 (Remember: in a major scale they’re between 3 and 4, and 7 and 1).
The second way to conceive of the minor scale is by taking a major scale and flatting (aka, lowering by a half-step) the 3rd, 6th, and 7th notes. We will write these from now on as b3, b6, and b7. This is important for reasons I will go into in a later post. You can think of a minor scale relative to a major scale like this:
Major: 1 2 3^4 5 6 7^1
Minor scale: 1 2^b3 4 5^b6 b7 1
Notice that by flatting the third note of the scale, you move it farther from 4 and closer to 2. This causes the half-step to move from between 3 and 4 to between 2 and 3. The same thing happens when you shift both 6 and 7 down a half-step.
TL;DR: A minor scale is made of 5 whole-steps and 2 half-steps. The half-steps fall between 2 and 3, and between 5 and 6. You can get a minor scale by flatting the 3rd, 6th, and 7th notes of a major scale. It can be written like this, where “^” means half-step: 1 2^b3 4 5^b6 b7 1.
Understand music theory without spending years learning the hard way 🎶
Grab our free 87-page eBook, Music Theory: The TL;DR Version – nail the fundamentals of melodies, chords, and notes the simple way 👇
Interval Basics
The word “interval” refers to the distance between two notes. The basic intervals are: Unison, 2nd, 3rd, 4th, 5th, 6th, 7th, and octave.
Each interval can be raised or lowered. We can divide the intervals into two groups:
Group 1: Unison, 4th, 5th, and octave
Group 2: 2nd, 3rd, 6th, and 7th.
Intervals in the first group are called “perfect.” Raising them by a half-step results in an “augmented” interval (for example, an augmented fourth). Lowering them by a half-step results in a “diminished” interval (for example, a diminished fifth).
The second group is the “major/minor” group. These intervals as referred to as “major” when they are untouched (Ex: a major third). If they are lowered by a half-step (aka “flatted”) then they are called minor intervals (Ex: a minor 6th).
Here’s the basic intervals and their distance:
|
Interval |
Distance |
|
Unison |
0 steps |
|
Diminished or flat 2nd |
1 half-step |
|
(Perfect) 2nd |
1 whole-step |
|
Minor 3rd |
1 whole-step + 1 half-step |
|
Major 3rd |
2 whole steps |
|
Perfect 4th |
2 whole steps + 1 half-step |
|
Augmented 4th/ Diminished 5th |
3 whole steps |
|
Perfect 5th |
3 whole steps + 1 half-step |
|
Minor 6th |
4 whole steps |
|
Major 6th |
4 whole steps + 1 half-step |
|
Minor 7th |
5 whole steps |
|
Major 7th |
5 whole steps + 1 half-step |
|
Octave |
6 whole steps |
Here are two examples of how each sounds, starting from a unison and going up by half-steps to an octave:
Melodically (notes played individually, back-to-back):
Harmonically (notes played simultaneously):
Side note: You will see varying notation and terminology for intervals. A diminished fifth can be written as “D5.” Guitarists tend to call a diminished fifth a “flat-five.” Just something to keep in mind.
We can also divide them into two different groups based on their consonant and dissonant nature:
Consonant intervals: unison, octave, all 3rds, some 4ths, 5ths, and all 6ths. (Don’t worry about the “some 4ths.” We’ll get to this later).
Dissonant intervals: all 2nds, some 4ths, all 7ths, and all augmented/diminished intervals.
One last note: It can be beneficial to think of a certain interval as a compound of two other intervals. For example, I think of a 5th as adding a minor 3rd and major 3rd. A 6th is a 5th with an added 2nd, etc. These are just cognitive tricks that will come with practice.
TL;DR: An interval is the distance between two notes. The basic intervals are: unison, 2nd, 3rd, 4th, 5th, 6th, 7th, octave. The perfect intervals are: Unison, 4th, 5th and octave. The major/minor intervals are: 2nd, 3rd, 6th, and 7th. The consonant intervals are: unison, all 3rds, some 4ths, 5ths, and all 6ths. The dissonant intervals are: all 2nds, some 4ths, all 7ths, and all augmented/dimin
The Minor Scale Expanded
First let’s refresh the natural minor scale formula. Where “^” denotes a half-step, the formula is:
1 2^b3 4 5^b6 b7 1.
However, there are two very common variations of the minor scale: harmonic and melodic. The simple explanation is that they lead better to the root note (the “1” of a scale). Here’s what harmonic minor sounds like:
And here’s the harmonic minor scale formula: 1 2^b3 4 5^b6 7^1.
Notice that there are three half-steps in this scale, rather than two. They occur between 2 and b3, 5 and b6, and 7 and 1. Also note that because the 7th is not flatted, the distance between b6 and 7 is not a whole-step, like it is in natural minor, but a whole-step and a half (three semitones).
Melodic minor is slightly more complicated. Melodic minor factors in the unusual gap (the three semitones) between the b6 and 7 and raises the 6th by a half-step. But here’s the catch: the 6th and 7th notes are raised in melodic minor only when it’s played ascending. If you’re going down a melodic minor scale, it’s played the same way as a natural minor scale.
Melodic minor ascending: 1 2^b3 4 5 6 7^1
Melodic minor descending: 1 2^b3 4 5^b6 b7 1
Here’s what the melodic minor scale sounds like, first ascending, then descending:
Don’t confuse this with harmonic minor, though. Harmonic minor is played the same regardless of whether it’s ascending or descending.
TL;DR: harmonic and melodic minor are two variations on the natural minor scale. The harmonic minor formula is: 1 2^b3 4 5^b6 7^1. The melodic minor formula depends on whether you are going up or down the scale. If you’re going up, it’s 1 2^b3 4 5 6 7^1; If you’re going down it’s the same as natural minor, 1 2^b3 4 5^b6 b7 1.
Pentatonic Scales
What are pentatonic scales?
Pentatonic scales are scales that have only 5 notes (the prefix “penta-” refers to the number five).
First, let’s look at the formulas and how they sound:
Pentatonic Major: 1, 2, 3, 5, 6
Pentatonic Minor: 1, b3, 4, 5, b7
So, how can you use pentatonics?
Pentatonic scales sound good. Like, really good. Pentatonic minor is commonly associated with blues and rock (Hendrix’s Voodoo Child, for example), but they’re found in every genre, including, of course, EDM. Justice uses pentatonic scales a ton. So does Mord Fustang. So does Tiesto. So does just about every musician, whether they realize it or not. So, play around with them. They’re incredibly flexible scales, and they aren’t limited to a particular “vibe” or “sound.”
But…why those notes?
(Warning: this is going to get a little dense, and you don’t need to know the “why” in order to use pentatonics effectively.)
The “backbone” notes of a scale, the notes that give a scale its basic qualities are the 1, 3, and 5. We (usually) want those notes in our scales. With that in mind, we can cut out “unnecessary” notes from a major and minor scale by eliminating notes that are a half-step away from any of those three notes. This is a pretty abstract concept,. I like to think of it like “we eliminate unnecessary notes so that there is more focus on the important ones—the 1, 3, and 5.”
So, let’s look at a major scale formula:
1 2 3^4 5 6 7^1
We can eliminate the notes that are a half-step away from 1, 3 or 5. Those notes are 4 (half-step from 3) and 7 (half-step from 1). Thus, we get pentatonic major: 1, 2, 3, 5, 6.
Same goes for the minor scale:
1 2^b3 4 5^b6 b7 1
Which notes are a half-step from 1, 3, or 5? 2 and b6. Thus, we get 1, b3, 4, 5, b7.
TL;DR: Pentatonic scales consist of 5 notes. They’re incredibly useful and sound amazing. The pentatonic major scale is: 1, 2, 3, 5, 6. The pentatonic minor scale is: 1, b3, 4, 5, b7.
Compound Intervals
Intervals that span a distance greater than an octave are called “compound intervals.” You can find out their number by adding 7 to the interval regular. Ex.: a “10th” is the distance of a 3rd an octave higher (3 + 7 = 10). We add 7 because there are 7 notes in a scale. This may seem confusing because a scale is usually thought of as 8 notes, but remember that the 8th “note” is just a repeat of the first note; it’s just an octave higher. So we add the interval to 7 rather than 8.
Here are the most common compound intervals:
9th, 10th, 11th, and 13th.
Here’s what these four sound like:
Melodically:
Harmonically:
(Note: 12ths and 14ths are possible, too, but less common in popular music).
If we plug them into our “interval + 7” formula, we get:
- A 9th is a 2nd, because 7 + 2 = 9
- A 10th is a 3rd because 3 + 7 = 10
- A 11th is a 4th because 4 + 7 = 11
- A 13this a 6th because 7 + 6 = 13
Compound intervals, like regular intervals, can be sharped or flatted. For example, jazz chords use a lot of “b9” (“flat-nine”) intervals in chords. Compound intervals come into play a lot in extended chords, but we’ll get to those soon.
TL;DR: Compound intervals are intervals greater than an octave. The most common ones are 9ths, 10ths, 11ths, and 13ths. The formula for a compound interval’s value is: (compound interval) – 7 = (interval value) or (interval) + 7 = (compound interval).
Understand music theory without spending years learning the hard way 🎶
Grab our free 87-page eBook, Music Theory: The TL;DR Version – nail the fundamentals of melodies, chords, and notes the simple way 👇
Inverted Intervals
So far we’ve only talked above ascending intervals, or intervals whose “base” or “root” note is the lower one. But what if the root note is the higher of the two notes? Then you get something called an “inverted” interval.
The formula to figure out an inversion is: 9 – (interval) = (inverted interval). However, once you’ve found the new number value, you must flip the major/minor and diminished/augmented quality of the interval. Perfect intervals stay perfect when inverted.
Ex: A major 3rd is an inverted minor 6th. 9 – 3 = 6, then switch the “major” to “minor.” A perfect fourth is an inverted perfect fifth because 9 – 4 = 5, and the quality (perfect) stays the same.
Here are some more:
| Ascending interval | Inversion |
| Minor 2nd | Major 7th |
| Major 2nd | Minor 7th |
| Minor 3rd | Major 6th |
| Major 3rd | Minor 6th |
| Perfect 4th | Perfect 5th |
| Augmented 5th | Diminished 4th |
| Perfect 5th | Perfect 4th |
| Minor 6th | Major 3rd |
| Major 6th | Minor 3rd |
| Minor 7th | Major 2nd |
| Major 7th | Minor 2nd |
| Octave | Octave |
The formula for inverting intervals works in the reverse manner, too. You can “un-invert” an inverted interval.
Ex: An inverted 4th is a regular 5th, and an inverted minor 7th is a major 2nd.
TL;DR: inverted intervals are intervals whose root note is the top note, rather than the bottom one. The formula for converting regular intervals to inverted ones, and vice versa, is: 9 – (interval) = (inverted interval).
If the interval is major/minor, or augmented/diminished, you must flip its quality. Major becomes minor, augmented becomes diminished, perfects stay perfect.
Triads
A triad consists of three notes: a root, a third, and a fifth.
Let’s look at a major triad first. It’s composed of a root, a 3rd, and a 5th (1, 3, 5). Triads like this are built by stacking thirds on top of one another. The distance between 1 and 3 is a third, and the distance between 3 and 5 is a third.
Note, however, that the third between 1 and 3 is a major third (1 2 3, two whole-steps), while the third between 3 and 5 is a minor third (3^4 5, one whole- and one half-step). Thus, we can think of the interval of a 5th as two stacked thirds: one minor, and one major.
In a major triad, the order of stacked thirds is (bottom) major, and (top) minor. But if we flip that order, we get a minor triad. A minor triad consists of 1, b3, and 5. The distance between 1 and b3 is a minor third (1 2^b3, one whole and one half-step) and the distance between b3 and 5 is a major third (3 4 5, two whole steps).
We also have diminished triads, which are formed by lowering the 5th note of a minor triad. Their formula is: 1, b3, b5.
We also have an augmented triad, which is formed by raising the 5th of a major triad: 1 3 #5.
Here’s what they sound like, in the order major, minor, diminished, augmented:
TL;DR: Triads are three note chords that consist of a root, third, and fifth. They can be major, minor, diminished or augmented. The formulas are: major: 1 3 5; minor: 1 b3 5; diminished: 1 b3 b5; augmented: 1 3 #5.
Chords
By definition, a chord consists of at least three different notes.
Notice the word “different;” an octave doesn’t count as a different note because it’s a repetition (so for you guitarists out there this means a power chord isn’t actually a chord).
Chords can be simple triads, but they can also be more complicated.
Rather than explain every possible chord out there, here are the most common ones and their formulas;
- Triads:
- Major: 1 3 5
- Minor: 1 b3 5
- Diminished: 1 b3 b5
- Augmented: 1 3 #5
- Suspended: 1 (2/4) 5
- 7th chords:
- Major 7th: 1 3 5 7
- Minor 7th: 1 b3 5 b7
- Dominant 7th: 1 3 5 b7
- Half-diminished 7th: 1 b3 b5 b7
- Diminished 7th: 1 b3 b5 bb7 (the double flat means it’s lowered a whole-step rather than a half-step).
I mentioned “suspended chords.” They’re important, especially for making the kind of chords you need a huge ethereal house anthem. A “suspended” chord refers to a chord that replaces it’s 3rd with a 2nd or 4th.
Here’s what each of the above chords sounds like, from top to bottom (major, minor, diminished, augmented, major 7th, minor 7th, dominant 7th, half-diminished 7th, diminished 7th):
Chords can be elaborated on a lot more than the ones I’ve mentioned, but we’ll get to that soon in another post.
TL;DR: Oh c’mon, this post isn’t even that long. Just read it.
Chord Voicing Variations
So far the chords we’ve talked about were built with the root as the lowest note (1 3 5, for example).
However, chords can be found in other patterns. When the root is on the bottom, the chord is in “root position.” When a note other than the root note is the lowest note, the chord is “inverted.”
When the third is the lowest note, the chord is in “1st inversion.” When the fifth is the lowest note, the chord is in “2nd inversion.” When the 7th is the lowest note, the chord is in “3rd inversion.” Here are what they sound like, starting off with a root position triad:
Beyond inversions, the notes of a chord can be spread out or rearranged. A chord doesn’t always have to be built in the order “1-3-5.” For example, you could raise the 3rd an octave up, and voice a chord: 1-5-10.
I find this works great for supersaws, because the third is often the main note that characterizes the sound of the chord. The root note gives your ear a foundation, the 5th strengthens and adds power, but the 3rd is the primary source of the harmonic quality. So putting the 3rd as the highest note can emphasize it strongly.
You can also double certain notes. For example, if you want a chord that sounds particularly strong, you could put two 5ths, an octave apart, and voice a chord: 5-1-3-5. These are just some ideas of variations. Chords don’t have to be 1-3-5. They can be rearranged and spread out over many octaves.
Here are what the two examples I mentioned sound like, a 1-5-10 voicing (from bottom to top) followed by a 5-1-3-5 voicing:
Another option is delaying certain notes of a chord. One trick I love doing that reminds me a lot of Wolfgang Gartner’s stuff is starting a chord with just a root and 3rd, and delaying the 5th, especially if it’s a 2nd inversion (meaning the 5th is the lowest note). Here’s what that sounds like:
TL;DR: Chords can be inverted. The 3 main classes of inversion are: 1st (the 3rd is the lowest note), 2nd (the 5th is the lowest note), and 3rd (the 7th is the lowest note). The notes of a chord can also be rearranged or spread wider than an octave.
Understand music theory without spending years learning the hard way 🎶
Grab our free 87-page eBook, Music Theory: The TL;DR Version – nail the fundamentals of melodies, chords, and notes the simple way 👇
Extended Chords
We’ve talked about triads and 7th chords, and extended chords build on those concepts. The three most common extended chords are 9ths, 11ths, and 13ths.
Now, as we know from the compound intervals section, a 9th is a 2nd an octave up, an 11th is a 4th an octave up, and a 13th is a 6th an octave up. So what we’re doing with extended chords is continually stacking 3rds onto our original 7th chord. Looking at the voicings should help you to understand:
9th chord = 1, 3, 5, 7, 9
11th chord = 1, 3, 5, 7, 9, 11
13th chord = 1, 3, 5, 7, 9, 11, 13
Note that those voicings can be minor, diminished, augmented, etc. (For example, a minor 11th chord = 1, b3, 5, b7, 9, 11).
Here’s what they sound like (in each, the first is an extended major chord, the second is an extended minor).
9th:
11th:
13th:
So how do we use extended chords? Listen to each of those chords, and toy around with them on your own. Ask yourself “how does this sound to me?” Personally, I find extended chords give an “ethereal,” “light” and “airy” feel. I like to use them for creating a big, floating feel in a trance or house drop. You’ll find them everywhere, though: Porter Robinson, Purity Ring, Eric Prydz, Tiesto, etc. They’re incredibly useful, and add a unique fullness to a song.
And, of course, you can invert them. Here’s a quick example, an 11th chord played normally, and then played with the 11th on the bottom:
And one quick last note. An important distinction in chord naming is the difference between an extended chord, and an “add” chord. The common question to figure out how well someone knows music theory is to ask, what’s the difference between a “9th” chord and an “add 9” chord. An “add 9” chord simply adds a 9th onto a triad. A 9th chord is an extended chord that includes all the notes a 3rd apart up to a 9th.
Better yet, here’s the voicings:
Add 9 = 1, 3, 5, 9.
9th chord = 1, 3, 5, 7, 9.
See what I mean? The 9th chord is an extended chord because it has all of the intervening note (the 7th). Not just the 9th.
TL;DR: Extended chords are built by stacking 3rds onto a 7th chord. The three fundamental extended chords are 9ths, 11ths, and 13ths. A chord with the word “add” is not an extended chord, but simply denotes you add the note (like an 11, in an “add 11” chord”) onto the original triad.
Partial Chords
What I mean by “partial chords” are chords that are missing a note or two. Remember that chords, by definition, have at least three different notes. We’ve talked about triads (chords consisting of only three notes) and 7th chords (chords including a 7th).
“Partial chords” are indispensable for changing the texture of your chord progressions (especially when you think about how many trance or house songs follow identical chord progressions!).
Your basic two options for “partial” chords are going to be taking out a 3rd or 5th. If we take out the 3rd of a minor 7th chord, we get the notes 1, 5, and 7. It sounds like this (first a full minor 7th chord, then minor 7th without a 3rd):
If we take out the 5th of a minor 7th chord, it sounds like this (full minor 7th chord, then minor 7th without the 3rd)
Both of those “partial” chords were in root position; Try inverting them, that’s where the real fun begins.
You can also take out the 3rd or 5th of a simple triad. Take notice that because it only has two different notes, it technically can’t be described as a “chord.” But it can sound just as awesome, especially if you “double up” one of the notes an octave up or down.
Here’s a triad, without the 5th note, and the 3rd note is doubled up an octave below:
Here’s a triad, without the 3rd note, with the 5th doubled up an octave below:
TL;DR: Try taking notes out of your chords, and doubling up others, to get varied textures.
Modes
We’ve touched on major and minor scales, but there’s another type of “scale.” It’s a little more abstract in nature, but incredibly useful, and you need to have a thorough understanding before moving on to more advanced theory concepts.
“Modes,” as they’re called, are the 7 variable patterns of the standard major/minor scale pattern. This can be a hard concept to wrap your mind around at first.
The idea is that the major scale contains a set pattern of whole and half-steps, right? But normally we play the major scale from the first note, 1, to the octave above. We normally go from 1 to 1 (or 8, if it makes more sense to understand the octave, but remember it’s just a repetition of the same note).
But what if, instead of starting and ending on the first note, we kept the same pattern of whole- and half-steps…but started and ended on the 2nd note? And then the 3rd? And then the 4th? We get 7 patterns, known as “modes.”
The 7 modes are, in order: Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian.
Here’s a chart to give you a better idea:
|
Mode |
Starting/ending note (relative to a major scale) |
|
Ionian |
1 |
|
Dorian |
2 |
|
Phrygian |
3 |
|
Lydian |
4 |
|
Mixolydian |
5 |
|
Aeolian |
6 |
|
Locrian |
7 |
Memorize these. Use mnemonics to help by coming up with a sentence where each word starts with the first letter of each mode: “I, D, P, L, M, A, L.” Do whatever you need to to remember the modes and their equivalent starting notes.
OK, so let’s look more in depth at each mode pattern, with their starting note relative to the major scale (which is the Ionian mode):
|
Ionian |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
|
Dorian |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
2 |
|
Phrygian |
3 |
4 |
5 |
6 |
7 |
1 |
2 |
3 |
|
Lydian |
4 |
5 |
6 |
7 |
1 |
2 |
3 |
4 |
|
Mixolydian |
5 |
6 |
7 |
1 |
2 |
3 |
4 |
5 |
|
Aeolian |
6 |
7 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Locrian |
7 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Now, if we remember that in the major scale half-steps occur between 3 and 4, and 7 and 1, we can establish a pattern of whole- and half-steps for each mode.
- Ionian: 1 2 3^4 5 6 7^1
- Dorian: 2 3^4 5 6 7^1 2
- Phrygian: 3^4 5 6 7 ^1 2 3
- Lydian: 4 5 6 7^1 2 3^4
- Mixolydian: 5 6 7^1 2 3^4 5
- Aeolian: 6 7^1 2 3^4 5 6
- Locrian: 7^1 2 3^4 5 6 7
But it makes more sense, for example, instead of imaging Lydian as “starting on the 4th note of a major scale,” to instead imagine it as its own scale, with its own formula.
So if we “re-align” the modes so that they each keep the same patterns of steps, but each starts on “1” (not the 1st of the major scale, but the first note of the mode pattern), then we get the following formulas:
- Ionian: 1 2 3^4 5 6 7 ^1
- Dorian: 1 2^b3 4 5 6^b7 1
- Phrygian: 1^b2 b3 4 5^b6 b7 1
- Lydian: 1 2 3 4^5 6 7^1
- Mixolydian: 1 2 3^4 5 6^b7 1
- Aeolian: 1 2^b3 4 5^b6 b7 1
- Locrian: 1^b2 b3 4^b5 b6 b7 1
Note: “Ionian” is the same as major scale and “Aeolian” is the same as minor scale.
The above seven formulas are the most important part of this post. Memorize them. We’ll get into more how to use modes in a later post, but you can start experimenting now. An easier way to remember them is to think of each as some variation on a major or minor scale. For example, here’s how I imagine them:
- Ionian: 1 2 3^4 5 6 7 ^1: the major scale
- Dorian: 1 2^b3 4 5 6^b7 1: the minor scale with a natural 6th instead of a b6
- Phrygian: 1^b2 b3 4 5^b6 b7 1: the minor scale with a b2
- Lydian: 1 2 3 #4^5 6 7^1: the major scale with a #4
- Mixolydian: 1 2 3^4 5 6^b7 1: the major scale with a b7
- Aeolian: 1 2^b3 4 5^b6 b7 1: the minor scale
- Locrian: 1^b2 b3 4^b5 b6 b7 1: the minor scale with a b2 and b5
Modes are annoying to learn at first but they come in handy a lot for sprucing up your music (we’ll get to that later). For now, make sure you understand the formulas for each, and spend time playing each to get a feel for how each sounds.
TL;DR: Modes are important. They are the 7 different possible patterns that you can get from the standard major scale whole- and half-step pattern. The 7 are: Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian. See above for formulas.
How Keys Work
In Western music, C major is the natural major scale. This means that the half-steps naturally occur between E and F, and B and C.
For example: C D E^F G A B^C.
Note that E and F are the 3rd and 4th, and B and C are the 7th and root. This follows our major scale formula, where half-steps are between the 3rd and 4th and 7th and root. If you look on a piano, the naturally occurring half-steps (where there is no black key) are between E and F, and B and C.
But what if, for example, we want to play in the key of F? Without changing any notes, if we start and end on F, we get this pattern:
F G A B^C D E^F
Without changing any notes, our half-steps fall between 4 and 5 and 7 and 1. But we want them between 3 and 4, and 7 and 1. So, we flat the 4th note (the B) to get:
F G A^Bb C D E^F
Now our half-steps fall between 3 and 4, and 7 and 1. So we can say that, in the key of F major, we have one flat, Bb. The same happens with keys involving sharps. Let’s look at the key of D major:
D E^F G A B^C D
Without changing any notes, the half-steps fall between 2 and 3 and 6 and 7. But again, we want them between 3 and 4, and 7 and 1. So we raise the 3rd and 7th notes:
D E F#^G A B C#^D
Now our half-steps fall between 3 and 4, and 7 and 1, which is what we want. We had to sharp both F and C and so we can say the key of D major has two sharps, F# and C#.
This is the idea behind “keys.” We have to change the quality of some notes by lowering them a half-step (flatting them) or raising them a half-step (sharping them) in order to make them fit the major scale formula.
TL;DR: The naturally occurring half-steps in Western music are between E and F, and B and C. To make keys other than C major fit the major scale formula, we have to alter certain notes by either flatting or sharping them.
Understand music theory without spending years learning the hard way 🎶
Grab our free 87-page eBook, Music Theory: The TL;DR Version – nail the fundamentals of melodies, chords, and notes the simple way 👇
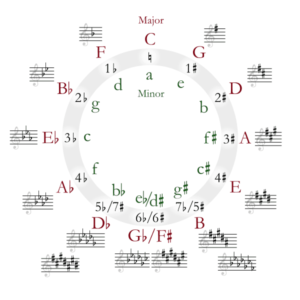
The Circle of Fifths
The circle of fifths is your friend. Then again, you could ignore it and just write everything in the key of C, like some producers. But that’d be like only using the preset EQ’s that your DAW comes with, without actually understanding any of them. It might not come to you the first time through this post, so re-read and play with the ideas, read other posts on the net, practice writing it out, and come back and re-read until you get it. It’s an incredibly important tool in music theory. It’s like setting up templates for tracks to improve your work flow.
The circle of fifths is the systematic representation of all major keys. It looks like this:
Last article we talked about how “keys” work. The circle of fifths is a systematic representation of those keys. It makes your life a lot easier, trust me.
It’s called the circle of fifths because it moves in fifths (or inverted 5ths, aka 4ths, depending which direction you’re going). For example, C is a fifth below G. G is a fifth below D, and D is a fifth below A, etc.
You should memorize the order of keys, in both directions. Here’s how I think of it: you always start with the key of C (no sharps or flats). If you want to figure out a key with flats in it, you go left, and start with F (because the word “flat” starts with “F”).
After “F” the keys are all flat (their root note is flat, like Bb) and they spell out “BEAD.” After BEAD, the last two keys in that direction are Gb and Cb. So for keys with flats, we get the pattern: C-F-Bb-Eb-Ab-Db-Gb-Cb.
And note that each of those keys goes up by one flat. C has no flats, F has one flat, Bb has two flats, Eb has three flats, all the way until Cb, which has 7 flats.
To go the opposite way, just flip that “F-BEAD-GC” pattern around, and sharp the last two keys. We get: C-G-D-A-E-B-F#-C#. Again, C major has no sharps, G has one sharp, D has two sharps, all the way until C# which has 7 sharps.
But how do we know which notes are sharp or flat? By two patterns called the order of sharps and flats.
- Order of sharps: FCGDAEB
- Order of flats: BEADGCF
Hey wait, isn’t that the same pattern as the order of keys themselves? Yep, it just starts at a different point. The circle of fifths has “C major” as its base, while the order of sharps starts on F, and the order of flats starts on B.
So, for example, say we’ve want to find out how many sharps E major has. We go to the circle of fifths and say, okay, E major is the 5th major key in the sharp pattern (C-G-D-A-E).
Since C major has no sharps, the sharp pattern begins on the 2nd key (G). So G has one sharp. And each following key has one additional sharp. So, since E is the 5th key in the pattern of keys with sharps, it has 4 sharps. Then we look at the order of sharps and take the first four sharps to find out which notes are sharp in E major: F, C, G, and D.
Here’s another example: how many flats does the key of Eb have? Well, if we look at the circle of fifths, the flat pattern is: CFBEADGC. The key of Eb would thus be the 4th key in the flat key pattern. Thus, Eb has three flats.
We can then look at the pattern of flats, and say, okay, this key has three flats, so the flatted notes will be the first three from the order of flats: Bb, Eb, and Ab.
The circle of fifths is hard to grasp at first, so don’t worry if you struggle the first time through. Re-read, check out other resources on the net, come back to it in a few days, or do whatever you need until you understand it. It’s an incredibly important foundation of music theory.
As always, if you have any questions or if anything was unclear, please comment and I’ll clarify. If you didn’t fully understand something, chances are someone else didn’t too!
TL;DR: The circle of fifths is incredibly important and can’t be “TL;DR”ed. Learn it. The order of “sharp” keys is: C, G, D, A, E, B, F#, C#. The order of “flat” keys is: C, F, Bb, Eb, Ab, Db, Gb, Cb. The order of sharps is: FCGDAEB, and the order of flats is: BEADGCF.
If you’re interested, we have a full guide on the circle of 5ths and how to memorize it here 🔥
A Tip on Intervals
One of the best tricks I learned from a former teacher was a quick trick to figuring out thirds and fifths. Memorize this pattern: C E G B D F A C. And backwards: C A F D B G E C.
Quick mnemonic for it: “FACE-GBD.” (You don’t have to start on C; it’s more a trick for interval recognition).
Notice the distance between each note is a third in that pattern. C to E is a major third, E to G is a minor third, etc. They’re all thirds, regardless of if they’re major/minor.
And what happens when we stack two thirds? We get the interval of a fifth. Thus, C to G is a fifth, E to B is a fifth, etc.
When doing it backwards, keep in mind the inverted nature of the pattern. You’re going down in thirds, not up. So, if you go down two steps (two thirds), you don’t get a fifth, you get a fourth, because it’s inverted (see inverted intervals).
You can also figure out 7ths: the 7th note relative to C is B, for example. Just stack three thirds to find it (C to E, E to G, and G to B).
This is just a really, really, REALLY handy trick to being able to quickly figure out what the notes of a chord are.
TL;DR: memorize the pattern C E G B D F A C, forwards and backwards. It’s notes a third a part, and it’ll make your life a lot easier.
So there you go, kiddos. Burn those in your brain until you’re having dreams (or nightmares?) of them, because once you understand those and can move onto the intermediate concepts, things get really interesting really fast.
Understand music theory without spending years learning the hard way 🎶
Grab our free 87-page eBook, Music Theory: The TL;DR Version – nail the fundamentals of melodies, chords, and notes the simple way 👇